Finance, at its core, revolves around several key principles that form the foundation of decision-making in both personal and corporate finance. Among the most important concepts that finance professionals must master are the Time Value of Money (TVM), risk, and return. These concepts help individuals and businesses evaluate opportunities, allocate resources, and manage uncertainty in a constantly changing market environment.
In this chapter, we will explore these fundamental financial concepts in depth, explaining how they influence financial strategies and decision-making.
The Time Value of Money (TVM)
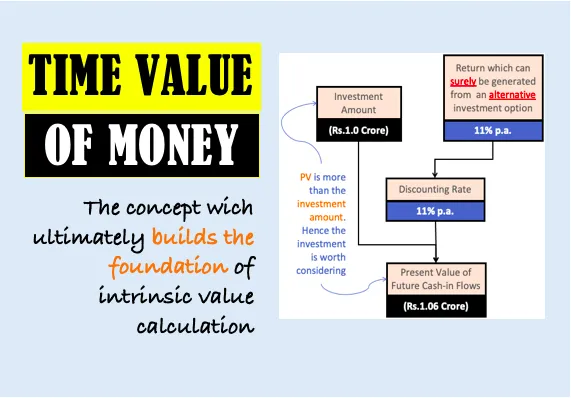
The Time Value of Money is the idea that a dollar today is worth more than a dollar in the future due to its potential earning capacity. This core concept is fundamental to financial planning, investments, and decision-making. Understanding how to measure the value of money over time allows individuals and businesses to make better financial decisions about investments, loans, and savings.
Present Value (PV) and Future Value (FV)
Two of the key calculations in the Time Value of Money are Present Value (PV) and Future Value (FV).
- Present Value (PV): This refers to the value today of a sum of money that will be received or paid in the future, discounted at a specific interest rate. It helps determine how much future cash flows are worth in today’s terms.
- Future Value (FV): Future Value is the amount an investment or savings will grow to in the future, based on a given interest rate. It reflects how money invested today will compound over time.
For example, if you have $1,000 today and invest it at an interest rate of 5%, in one year it will grow to $1,050. The ability of money to earn interest is what drives the concept of future value, making $1,000 today more valuable than $1,000 in the future.
The formula for calculating Future Value is:
[
FV = PV \times (1 + r)^n
]
Where:
- PV = Present Value
- r = interest rate
- n = number of periods (years, months, etc.)
Similarly, Present Value is calculated by:
[
PV = \frac{FV}{(1 + r)^n}
]
These equations allow finance professionals to assess the value of investments, calculate loan repayments, and make decisions about future financial obligations.
Discounting and Compounding
The processes of discounting and compounding are integral to understanding TVM.
- Compounding: This refers to the process by which an investment grows over time as interest is earned on both the initial principal and the accumulated interest from previous periods. The more frequently interest is compounded (daily, monthly, or yearly), the greater the future value of the investment.
- Discounting: In contrast, discounting is the process of determining the present value of a future sum of money. It is used to evaluate investment opportunities and to make decisions about which future payments or cash flows are worth pursuing today.
Annuities and Perpetuities
An annuity is a series of equal payments made at regular intervals over a period of time, such as mortgage payments or insurance payouts. In finance, understanding how to value annuities is essential for retirement planning, loan structuring, and evaluating financial products like bonds.
- Ordinary annuity: Payments are made at the end of each period.
- Annuity due: Payments are made at the beginning of each period.
A perpetuity, on the other hand, is an annuity that lasts forever, with payments continuing indefinitely. Perpetuities are often used in the valuation of certain financial instruments like preferred stock, which pays a constant dividend in perpetuity.
The Present Value of an Annuity (PVA) can be calculated using:
[
PVA = C \times \left(\frac{1 – (1 + r)^{-n}}{r}\right)
]
Where:
- C = Cash flow per period
- r = interest rate
- n = number of periods
For a perpetuity, the Present Value is:
[
PV = \frac{C}{r}
]
These formulas are fundamental in making long-term financial planning decisions, whether you’re dealing with investments, loans, or retirement plans.
Risk and Return
In the world of finance, risk and return are inseparable. Every financial decision involves balancing potential rewards with the risks that come with it. The relationship between risk and return is critical in determining the viability of investments, as investors generally require a higher return to compensate for higher levels of risk.
Types of Risk
- Systematic Risk:
This is the risk inherent to the entire market or market segment. It is also known as market risk or undiversifiable risk because it cannot be eliminated through diversification. Systematic risks include factors such as economic recessions, interest rate changes, political instability, or global events like pandemics. Investors can’t control these risks but must account for them when evaluating potential returns. - Unsystematic Risk:
Also known as specific risk or diversifiable risk, this type of risk is associated with individual companies or industries. For example, a company might face operational risks, product recalls, or management issues, all of which could impact its stock price. Investors can reduce unsystematic risk through diversification by holding a wide variety of investments in different sectors. - Credit Risk:
This is the risk that a borrower will default on their financial obligations. It is particularly relevant for lenders and bondholders, who need to assess the creditworthiness of the entities to which they lend money. - Liquidity Risk:
Liquidity risk refers to the risk that an investment cannot be sold quickly without a significant loss in value. Some assets, like real estate, can be illiquid and may take time to convert into cash, which poses a risk in cases where immediate liquidity is needed. - Inflation Risk:
Inflation erodes the purchasing power of money over time. For example, if an investment earns a 3% return but inflation is 4%, the investor has effectively lost money in terms of real purchasing power. Investments that don’t keep pace with inflation carry inflation risk.
The Risk-Return Tradeoff
The risk-return tradeoff states that the potential return on any investment increases with an increase in risk. Investors demand higher returns for taking on higher levels of uncertainty. For example, stocks typically offer higher returns than bonds because they come with higher risk, such as price volatility and market fluctuations.
In evaluating risk and return, finance professionals use several tools:
- Expected Return: This is the average return that an investment is expected to generate based on historical data or future projections. It helps investors estimate the potential gains from an investment.
- Standard Deviation (Volatility): Standard deviation measures the variability of returns from an investment. The higher the standard deviation, the higher the investment’s volatility, meaning it has a higher level of risk.
- Beta: Beta is a measure of an investment’s volatility relative to the overall market. A beta of 1 indicates that the investment’s price will move with the market. A beta greater than 1 suggests higher volatility, while a beta less than 1 indicates less volatility compared to the market.
The Capital Asset Pricing Model (CAPM)
The Capital Asset Pricing Model (CAPM) is a widely used formula in finance that helps investors understand the relationship between risk and expected return. CAPM shows that the expected return of a portfolio or individual security depends on its risk (measured by beta) and the risk-free rate of return (such as government bonds).
The formula for CAPM is:
[
E(R_i) = R_f + \beta_i (E(R_m) – R_f)
]
Where:
- E(R_i) = expected return of the investment
- R_f = risk-free rate
- β_i = beta of the investment
- E(R_m) = expected return of the market
CAPM helps investors determine whether an asset provides a satisfactory expected return, given its level of risk.
Conclusion
The principles of Time Value of Money, risk, and return form the bedrock of financial decision-making. Understanding how money grows over time, how to balance potential rewards against risks, and how to apply models like CAPM are essential skills for any finance professional. These core concepts enable businesses and individuals to make informed investment decisions, manage risk effectively, and maximize financial performance over time.
In the next chapter, we will explore financial statement analysis and interpretation, a crucial skill that helps finance professionals understand a company’s financial health and make sound investment decisions.